ECC 椭圆曲线加密算法学习————安全性问题与实战
标签(空格分隔): ecc Crypto
****
> File Name: ECC 椭圆曲线加密算法学习————安全性问题与实战
> Author: shaobaobaoer
> Mail: shaobaobaoer@126.com
> WebSite: shaobaobaoer.cn
> Time: Sunday, 24. March 2019 11:05PM
****
0x00 前言
之前学习了ECDSA 和 ECDH 算法。不难发现椭圆曲线的离散对数难题对该密码的安全性有着多么重要的作用。之前谈及,椭圆曲线的离散对数难题非常难,尽管如此,也应该有些方法可以解开这个问题。就好像对于模运算的密码系统,比如RSA而言,可以用yafu工具来强解,也可以上某网站查表,也包括一些共模攻击,小指数攻击等方法。
参考的网站
- https://andrea.corbellini.name/2015/06/08/elliptic-curve-cryptography-breaking-security-and-a-comparison-with-rsa/
- https://github.com/p4-team
相关代码
0x01 BSGS 小步大步法
方法的英文名是Baby-step, giant-step,这个算法基于一个非常简单的道理
$$Q = xP = (am +b)P \Longrightarrow Q -amP = bP$$
1.1 算法简介
BSGS方法的步骤就是中间相遇。算是一种比较机智的暴力搜索法。该算法的工作步骤如下。
对于知道公钥和域参数六元组的情况下
- 计算 $m = \sqrt{n}$
- 对于 $b={0..m}$,计算$bP$并打表
- 对于 $a={0..m}$
- 计算 $Q - amP$
- 寻找与 上式子结果相同的 $bP$
- 如果找到,那么$k=b + am$
那么所谓的baby其实就是b。而gaint 就是 am。参考某作者的一张图片,可以很清晰的阐明这个思路。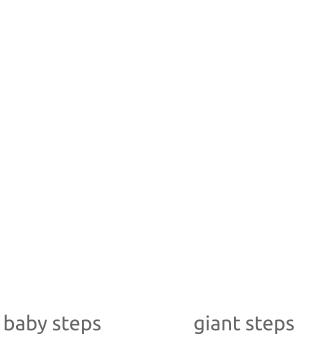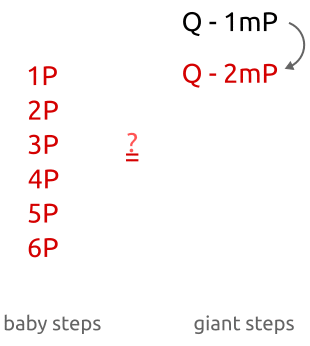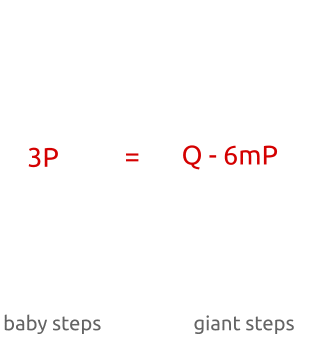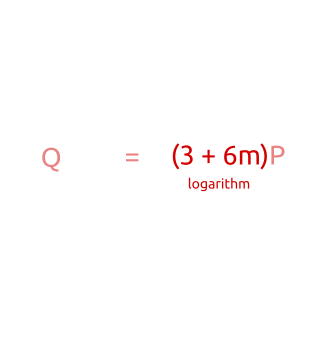
之所以取 $m = \sqrt{n}$ 是因为这样可以取遍所有 n的情况
- 对于 $a = 0 ; Q = (0m + b)P$ 这样就去遍历了所有 $Q = (1..m)P$ 的情况
- 对于 $a = 1 ; Q = (m + b)P$ 这样就去遍历了所有 $Q = m + (1..m)P$ 的情况
- …
- 对于 $a = m-1 ; Q = (m-1 + b)P$ 这样就去遍历了所有 $Q = (m)m + (1..m)P$ 的情况
之后来看下其复杂度,如果认为查表的速度为O(1),那么该算法的时间复杂度和空间复杂度是$O(\sqrt{n})$
实际上这还是一个非常大的数字。
对于prime256v1而言,$\sqrt{n}$大概为$3.402823669209385 \times 10^{38}$。即使是哈希表的每个节点占1B,那也必然是Memory Error。
1.2 算法实践
之后可以简单实践以下这个算法
1 | def BSGS(E, p, q): |
对于这样的测试样例,很快就可以算出来了。(我算了102步)
1 | E = EllipticCurve(a=1, b=-1, p=10177, GF=10331) |
0x02 Pollard rho 算法
刚才谈及,小步大步算法的空间复杂度太高,对于大参数曲线无法使用。因此得想些别的办法。pallard rho算法就是解决了这样的问题,时间复杂度与BSGS一样(但是理论上BSGS更快),空间复杂度只有$O(1)$
其核心思想是找到满足 $aP+bQ=AP+BQ$的参数$a,b,A,B$
对于 $Q = xP$ 有如下等式。
$$aP+bQ=AP+BQ\
aP+bQ=AP+BxP\
(a+bx)P=(A+Bx)P\
(a−A)P=(B−b)xP$$
如果要约去 $P$,需要加上取余符号。这步骤有点类似与同k的x计算方法。将x独立出来,可以得到
$$x \equiv (a-A) \times (B-b)^{-1}; mod; n $$
这样就可以算出$x$了
那么如何取确定$a,b,A,B$呢?之前说过,椭圆曲线的标量积满足分配律。这就意味着,如果定义一串伪随机数序列$(a_n,b_n)$,因为$P$和$Q$的标量积是有循环性质的,所以$aP+bQ$也是循环的。
当我们产生出这样一个循环序列后,从该序列中任取一组$(a,b)$随后更具循环序列的性质,找到满足$aP+bQ=AP+BQ$的$A$与$B$即可。
2.1 计算循环序列
非常糟糕的是,如果对所有a,b进行遍历,所需要的复杂度是$O(n^2)$显然这不能满足需求。而实际上有一种算法能够很好的解决这样的问题。该算法称为乌龟野兔算法,也称为弗洛伊德发现算法。
其算法大意就是定义两个点,分别对应(a,b)和(A,b),一个点(乌龟)每个时间步前进一格,也就是逐一读取伪随机序列中的点。另一个(兔子)每个时间步前进两格,也就是一个跳一个读取伪随机序列中的点。如果点的范围超出了循环子群的阶n。那么对其进行取余操作。
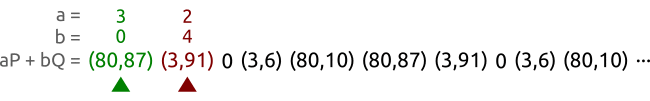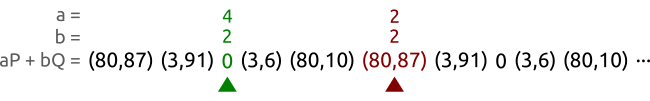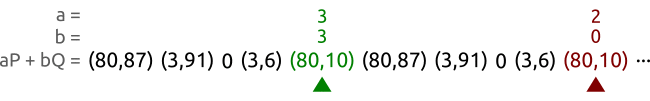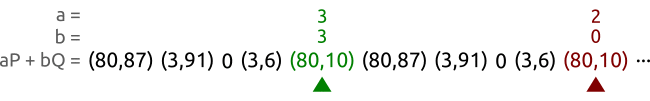
如图所示,对于曲线$y^2≡x^3+2x+3;(mod;97)$ 首先它的循环子群阶为5。定义两个点 (a,b)。 和 (A,B) 绿色的代表乌龟,红色的代表兔子。很快就能找到两个相同的点。
如果随机序列是静态存储的话。那么空间复杂度就是 $O(1)$。如果随机序列是动态生成的话,那么空间复杂度大概是是$O(logn)$。计算渐进随机序列的时间复杂度非常困难,利用概率证明来证明时间复杂度的话,可以得到$O(\sqrt(n))$。
2.2 算法实践
修了修原文作者造的轮子,于是就能用了。他随机序列方法和图中有些不太一样,大概就是采用+;*;+的顺序。感觉挺有意思的,有兴趣的话可以去我的github底下看看。最终的结果为
1 | E = EllipticCurve(a=1, b=-1, p=10177, GF=10331) |
0x03 量子算法 Shor
很显然,哪怕把复杂度降低到$O(\sqrt n)$,仍然也解决不了数学难题,那未来的技术呢?确实存在一种能够在多项式时间内计算离散对数的量子算法:Shor算法,具有时间复杂度$O((logn)^3)$ 和空间复杂性 $O(logn)$。
量子计算机时至今日,仍然远未变得足够复杂来运行诸如Shor的算法,需要量子抗性算法的深入得研究
0x04 SageMath 工具
后来我从P4队的WP里看到了这个很牛逼的工具。里面的椭圆曲线求对数函数的速度非常快。我不太知道他用了什么方法,应该是改进的 rho 吧。
下载地址
http://www.sagemath.org/download.html
实际上这是一个用python2.7写的数学计算库。椭圆曲线的东西用起来非常舒服
大概的步骤如下所示,比我造的轮子好用多了。
1 | sage: E =EllipticCurve(GF(10177),[1,-1]) |
0x05 ECC VS RSA
首先抛弃一下量子计算,为什么ECC比RSA优秀呢?NIST给了个表,告诉我们实现相同的安全级别,所需要的RSA与ECC的比特数
| RSA key size (bits) | ECC key size (bits) |
|---|---|
| 1024 | 160 |
| 2048 | 224 |
| 3072 | 256 |
| 7680 | 384 |
| 15360 | 521 |
请注意,RSA密钥大小与ECC密钥大小之间没有线性关系(也就意味着:如果我们将RSA密钥大小加倍,并不需要将ECC密钥加倍)。该表不仅告诉我们ECC使用更少的内存,而且密钥生成和签名也要快得多。
但为什么会这样呢?答案是,用于计算椭圆曲线上离散对数的更快算法是Pollard rho和BSGS,而在RSA的情况下,有着特殊的对抗算法,比如通用数字域筛,它用于整数因子分解的算法(yafu就是用的这个)。一般数字域筛是迄今为止最快的整数分解算法。该算法正对所有适用于基于模运算的其他密码系统,包括DSA,DH和ElGamal。
0x06 CTF题目实战
XUSTCTF 2016
1 | 已知椭圆曲线加密Ep(a,b)参数为 |
算是一个非常常规的题目了。直接用自己写的轮子就可出了
1 | from curve_base_class import EllipticCurve |
HXP 2018 Curve12833227
WP:https://github.com/p4-team/ctf/blob/master/2018-12-08-hxp/crypto_curve12833227/vuln.py
关键代码如下,省略了mul和add两个函数。
1 | from random import randrange |
Securinets CTF Quals 2018 Improve the quality
这个题目一开始给了个很长很长的描述。简单概括一下就是
- 已知曲线 $ y^2 = x^3 + A*x + B$
- 已知 A = 658974
- 不知道 B 但是它最重要的数字是6
- p = 962280654317
- 生成元 P = (518459267012, 339109212996)
- 私钥位 k。将k 切成若干份
- Qi = ki * P
- 以及一大堆的$Q_i$
首先先把B算出来
1 | B = (P[0] ** 3 + A * P[0] - P[1] ** 2) % p |
这样算B会很大,加法逆元一下,得到B=618 满足条件。
这里需要用到之前介绍的sagamath工具。把Q中的点遍历一遍,就可以很快求出结果
1 | K.<z> = GF(prime) |
之后把数字转chr即可获得一段提示,根据提示找到一张图片,解隐写可得FLAG。
1 | for i in solutions: |
ASIS Final 2016 RACES
这个加密算法,看上去没有什么大问题,这么多密钥参数,很容易让人想到是共模攻击。
突破点在于其素数生成函数
1 | prime = getPrime(nbit) |
这也就意味着,这里面所有的素数都是被3模余2的。我们知道素数只有$6k+5$和$6k+1$的形式(这是个伪命题),这也就意味着该脚本中的素数都是$6k+5$的形式。
在公钥文件里面,包含了非常多的(n, e),其n来自于利用该方法生成的两个素数之积。对于这种题目的一般做法是查看两个公钥是否有相同的参数,这个题目也不例外。
1 | for pair in tqdm.tqdm(itertools.combinations(pairs, 2)): |
这样,就能够找到p,q的值,并且迅速定位到c的值。
脚本中的加密过程非常简单,只不过是加了个ECC的壳子而已
∵$d = e^{-1} ;mod ;lcm$
∴$C = eM \Longrightarrow M = dC$
所以只需要求出e的逆元就可以了。
1 | lcm = gmpy2.lcm((p + 1), (q + 1)) |
最终一波解密可以得到FLAG。
TUM CTF 2016 Heicss
我改编了一些东西
虽然归属了椭圆曲线的tag。但是只是涉及了一些基本的操作
首先那个order有点脑洞。我自己爆爆了半个小时也没有个所以然来,所以直接给正确的order了。感觉当初官方应该给了个hint,说实际的order和脚本的order差了在末尾的若干个空格,正确的order就是原本脚本里的order加四个空格
主要代码如下
1 | Give me the flag. This is an order! |
不难发现,输入的被拆为 前64和后64到最后的两个部分,第二部分通过了 SHA256 加密生成了 h。
首先来跟踪前40位的部分
- 再输入长度超过64位,并且签名错误的情况下
- 如果 s >= q 那么会打印bad signature
- 如果 s < q 那么会打印bad signature 以及 前半部分还有后半部分经过一个函数变换后的值。
就好像盲注一样,s已知可以通过二分盲注来爆破出q的值
这个不会非常困难。由于我没有环境部署这个题目,就暂且跳过了。爆出来的q是这样的
1 | q = 0x247ce416cf31bae96a1c548ef57b012a645b8bff68d3979e26aa54fc49a2c297 |
随后,记 s 为 S 的横坐标,随后会计算S的纵坐标(我姑且这么解释),纵坐标就是以下方程的一个解
$$y ^ 2 \equiv x^3 + ax +b ; mod ; q $$
当然,由于横坐标可以任意定。如果取0的话,那么y就变成了
$$ y^2 \equiv b; mod ; q $$
这个y是可以打印出来的
1 | >> 00000000000000000000000000000000000000000000000000000000000000001 |
这样的话,就可以计算出b的值
1 | b = 8575167449093451733644615491327478728087226005203626331099704278682109092640 |
如果尝试输入1,那么会使得y无法算出来,应该是 GCD == 1 了。
那么,如果输入的横坐标是2的话,那么y就变成了
$$ y^2 \equiv (8 + 2a + b); mod ; q $$
这样的话,就可以计算出a的值
1 | >> 00000000000000000000000000000000000000000000000000000000000000021 |
目前得出了椭圆曲线的几个参数,分别是$ a,b,p,$还有生成元$S$。
- S的横坐标是输入的x,纵坐标是将x带入曲线方程中得到的y
那么就要来观察一下签名部分了。
已知签名的内容来自于输入的字符串从第64位开始到最后,采用了 SHA256的加密得到 $h$
如果 $(e S )x = h$ 那么会返回m。我们需要的是让m为order,也就是最顶上的那个字符串。
很显然,只有S是可控的。并且h是已知的,为了方便,我们需要让两个坐标点相等,而不是傻乎乎得去把S的横坐标取出来和h比较。(这也是为啥我说官方应该给了hint,wp里说最后的msg应该加上四个空格,我看了好久都没看懂…)非常巧合的是可以利用模的逆元来算出S
$$ S = e^{-1}*h$$
如果要算e的逆元,那么就需要知道椭圆曲线的阶是多少。令我非常费解的是,椭圆曲线循环子群的阶是如何算出来的。这个数字太大了导致我用schoof算法直接内存爆了。
这边非常无奈的抄一下答案
1 | feild_order = 16503925798136106726026894143294039201930439456987742756395524593191976084900 |
于是,一串小脚本就可以算出 S 了。
1 | e = 65537 |
取出横坐标,非常巧合得发现其横坐标刚好64位也不用补0啥得。
1 | "10feab68fea4ecbc95e2f7c67ebcf83e75fc0e0357006ca2429559f4aa83fce8".__len__() |
把它和最前面那段加起来,即可得到结果
1 | 10feab68fea4ecbc95e2f7c67ebcf83e75fc0e0357006ca2429559f4aa83fce8Give me the flag. This is an order! |